von Jona Dirks

Bestimmt ein ganz einfaches Rätsel! Oder vielleicht auch nicht? Quelle: Eigene Graphik und Pixabay
Du denkst, Informatiker*innen sitzen den ganzen Tag vor‘m Computer und sehen lustige Zahlenreihen über den Bildschirm tanzen? Falsch gedacht! Für den Rätselspaß der Graphtheorie genügen erstmal Stift und Papier – oder eine Wäscheleine und ein paar Bäume.
Vielleicht kennst du das folgende Rätsel: Es gibt drei Häuser und jeweils ein Gas-, Wasser- und Stromwerk. Jedes der Häuser soll an Gas, Wasser und Strom angeschlossen werden. Die Leitungen sollen aber alle auf derselben Höhe gebaut werden, dürfen sich also nicht überschneiden. Versuche doch einmal selbst, ob du eine Lösung findest:
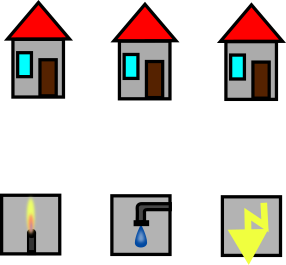
Abbildung 1 – Rätsel: Alle Häuser sollen an die Versorger (Gas, Wasser und Strom) angeschlossen werden. Die Leitungen sollen sich dabei aber nicht überkreuzen. Wie kann das gelingen? Quelle: Eigene Abbildung
Ich bin mir sicher, dass du keine Lösung gefunden hast. Ich übrigens auch nicht. Während ich das bei mir noch auf meine Einfalt schieben kann, muss das bei dir ja andere Ursachen haben. Also, woran liegt das? Ok, dass ist einfach: Weil es keine Lösung gibt. Die entscheidende Frage ist doch: Warum gibt es keine Lösung?
Um diese Frage zu beantworten, machen wir einen Ausflug in die Graphtheorie. Ein Graph, das ist ein ganz simples Konzept. Er besteht aus Punkten, die über Linien miteinander verbunden sind. Wie hier zu sehen:
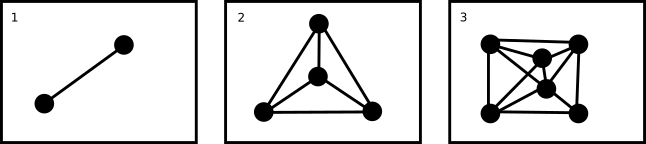
Abbildung 2 – Beispiele für Graphen. Quelle: Eigene Abbildung
Die Punkte nennen wir Knoten und die Linien Kanten.
Graphen können hier an sehr vielen Stellen als Vereinfachung eingesetzt werden. So können wir zum Beispiel Bahnhöfe als Knoten auffassen und Schienenverbindung zwischen diesen Bahnhöfen als Kanten. Oder alternativ: Fahrradwege und Straßen als Kanten und Kreuzungen als Knoten. Auch soziale Beziehungen lassen sich als Graphen ausdrücken. Knoten können dabei für Personen stehen und Kanten zum Beispiel für Freundschaften. Aber auch farbige Flächen und deren Berührungen können als Knoten und Kanten aufgefasst werden. Graphen sind also vielfältig einsetzbar und stellen eine wichtige Vereinfachung dar, die es sich lohnt genau zu untersuchen.
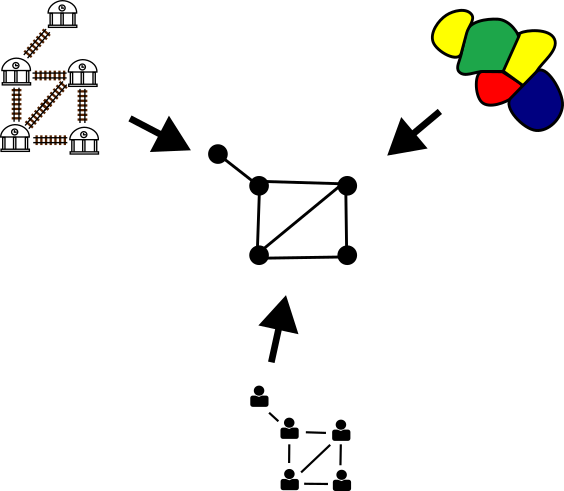
Abbildung 3 – All diese Beispiele können durch den gleichen Graphen beschrieben werden. Quelle: Eigene Abbildung
Aber nicht alle Graphen sind gleich. Einige haben bestimmte Eigenschaften. An dieser Stelle soll es nun um eine besonders wichtige Eigenschaft gehen: Die sogenannte Planarität. Wir bezeichnen einen Graphen als planar, wenn wir ihn aufzeichnen können, ohne dass sich Kanten überschneiden [1]. Von den Beispielen oben in Abbildung 2 wären also die ersten beiden Graphen planar.
| Infobox
Mengenschreibweise Seit gut einem Jahrhundert ist die Mengenlehre aus der Mathematik nicht mehr wegzudenken. Eine Menge ist eine Ansammlung von Teilen, ohne das diese weiter geordnet sind. Ein Teil kann also nur in einer bestimmten Menge vorkommen oder nicht. Auch Graphen sind in diese spezifische Schreibweise übertragen worden. So fassen wir die Knoten und Kanten in je einer Menge zusammen. Sollen Mengen benannt werden, werden häufig große Buchstaben genommen. Bei den Knoten ist dieses meist V, für das englische Wort „Vertices“ und bei Kanten E, für das englische Wort „Edges“. Ist, wie in unserem Fall, nur die Anzahl der Teile von Relevanz, so gibt es auch dafür spezielle Schreibweisen. Diese sind aber nicht einheitlich, oft werden aber vertikale Striche genommen. Die Anzahl der Knoten wird also mit |V| bezeichnet. |
Nun können wir anfangen, in diesen Graphen bestimmte Dinge zu zählen. Nämlich Knoten, Kanten und Flächen. Machen wir das doch einmal für Graph 2 in Abbildung 2: Relativ einfach lassen sich die 4 Knoten zählen. Mathematisch bezeichnen wir die Knotenanzahl mit |V|. Wir haben hier also |V| = 4. Auch die Kanten lassen sich gut zählen. Mathematisch notieren wir die Kantenanzahl mit |E|. Wir haben also |E| = 6.
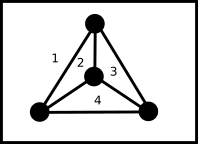
Abbildung 4 – Besonders interessant sind die Flächen! Wie viele Flächen besitzt dieser planare Graph? Quelle: Eigene Abbildung
Und bei den Flächen? 3 Flächen werden von den Kanten eingeschlossen und aufgepasst – wir müssen auch die äußere Fläche mitzählen. Also: |F| = 4 Flächen.
Hängen diese Zahlen vielleicht irgendwie zusammen? Nehmen wir die Kanten Anzahl und ziehen die Anzahlder Knoten ab. Danach addieren wir 2 darauf, so erhalten wir die Anzahl der Flächen:
|E| – |V| + 2 = |F|
ist
6 – 4 + 2 = 4
Zufall? Probieren wir das doch nochmal mit einem anderen Graphen aus:
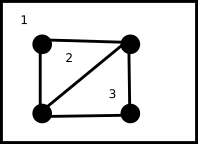
Abbildung 5 – Bestätigt sich auch bei diesem Graphen der Zusammenhang zwischen Knoten, Kanten und Flächen? Quelle: Eigene Abbildung
Hier haben wir |E| = 5, |V| = 4 und |F| = 3. Und auch hier gilt die gleiche Formel wie eben:
5 – 4 + 2 = 3
Tatsächlich gilt dieser Zusammenhang immer bei planaren Graphen, vorausgesetzt, sie sind zusammenhängend [1]. Zusammenhängend heißt dabei, dass der Graph ein Konstrukt ist und nicht aus zwei verschiedenen Teilen besteht, die gar nicht miteinander zusammen hängen.
Moment mal, damit das gilt dürfen sich also Linien nicht überschneiden? Sich nicht überschneidende Linien kommen uns doch von unserem Rätsel bekannt vor!
Bevor wir uns dem widmen, müssen wir uns noch eine Sache überlegen: Dass wir uns mit Häusern und Werken beschäftigen, ist komplett egal. Genauso gut könnten wir auch Wäscheleinen zwischen runden und eckigen Balken ziehen:
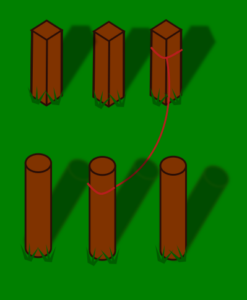
Abbildung 6 – Dasselbe in grün. Dieses Wäscheleinen-Rätsel ist ein vollständig bipartiter Graph. Quelle: Eigene Abbildung
Wichtig ist nur, dass wir zwei verschiedene Mengen haben und diese insgesamt verbinden. Hierbei sprechen wir auch von vollständigen bipartiten Graphen. „Bipartit“, weil wir unsere Knoten in zwei Mengen aufteilen können, ohne dass es Kanten innerhalb dieser Mengen gibt. „Vollständig“ sagen wir, weil wir alle erlaubten Kanten zwischen zwei Objekten ziehen. Dabei müssen wir jedoch beachten, dass Kanten zwischen zwei Objekten verschiedener Mengen verboten sind, damit der Graph bipartit bleibt.
Jetzt, wo wir das wissen, können wir uns mal überlegen, wie eine mögliche Lösung aussieht und die entscheidenden Kennzahlen bestimmen. Die Knoten sind einfach, wir können sie zählen: Es sind |V| = 6. Bei den Kanten müssen wir schon etwas rechnen. Wir haben jeweils 3 Werke und 3 Häuser und, weil wir alle Kombinationen daraus abdecken wollen, gibt es insgesamt 3×3=9 Kanten. Also |E| = 9.
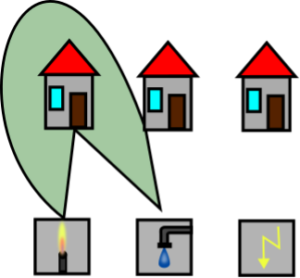
Abbildung 7 – Zurück zu dem Häuser-Rätsel: Wie viele Knoten, Kanten und Flächen haben wir hier? Quelle: Eigene Abbildung
Wie sieht das nun mit den Flächen aus? Hier zu müssen wir uns überlegen, dass immer zwei Werke und zwei Häuser ein Viereck bilden:
In diesen Vierecken kann weder etwas drin liegen, was Kontakt nach außen hat, noch kann irgendetwas hinein ragen. Wir können insgesamt folgende Vierecke bilden:
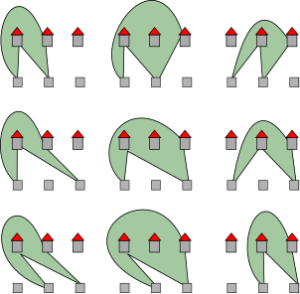
Abbildung 8 – Alle möglichen Vierecke in unserem Beispiel. Quelle: Eigene Abbildung
Wir haben also |F| = 9 Flächen. Setzen wir das nun in die Gleichung ein, sehen wir, dass
9 – 6 + 2 ≠ 9.
Also kann es keine Lösung für das Problem geben.
Probieren wir das nochmal für ein anderes Beispiel aus. Lassen wir doch ein Werk einfach mal weg:
Abbildung 9 – Neuer Versuch: Können wir das Rätsel diesmal lösen? Quelle: Eigene Abbildung
Jetzt haben wir |V| = 5 Knoten. 2×3 also |E| = 6 Kanten und [1,2,a,b] [1,3,a,b] [2,3,a,b] Flächen bzw. gezählt |F| = 3. Die Formel geht hier also wieder auf:
6 – 5 + 2 = 3
Und tatsächlich gibt es auch eine Lösung:
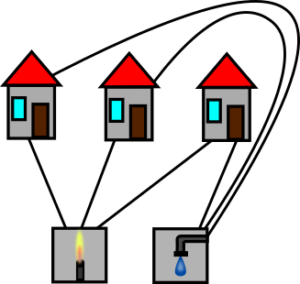
Abbildung 10 – Tatsächlich! Dies ist eine mögliche Lösung. Warum hat es diesmal geklappt? Quelle: Eigene Abbildung
Wir konnten hier sehen, dass planare Graphen bestimmte Eigenschaften haben, die für allgemeine Graphen nicht gelten — wie unsere Formel |E| – |V| + 2 = |F|. Das ist aber natürlich nur ein Beispiel, es gibt noch viel, viel mehr, was explizit nur für planare Graphen gilt. Wie wir gesehen haben, verbergen sich hinter Problemen aus der realen Welt nicht selten planare Graphen. Einige derer Eigenschaften sind insbesondere dann interessant, wenn wir diese Graphen mit dem Computer behandeln wollen.
Betrachten wir Graphen auf dem Computer, tun wir der Einfachhalt halber so, als ob uns nur interessiert, ob ein Graph bestimmte Werte besitzt. Ein einfaches Beispiel wäre, ob der Graph mehr als n Kanten hat. Dabei kann n jede beliebige ganze Zahl sein. Oder alternativ schaffen wir es, mit dem Einfärben von n Knoten dafür zu sorgen, dass jede Kante mindestens an einen farbigen Nachbar grenzt. Für einige dieser Entscheidungen können wir Computerprogramme schreiben, die dieses schnell herausfinden, für manche kennen wir nur sehr ineffiziente Programme. Manchmal können wir Programme effizienter gestalten, wenn wir wissen, dass der zu untersuchende Graph planar ist (vergleiche [2]).
Hier setzt meine Masterarbeit an: Es geht darum, für eine bestimmte Art von Entscheidung kombiniert mit einem kleinem n, ein schnelles Programm zu schreiben, dass funktioniert, wenn der Graph planar ist. Diese Arbeit schreibe ich in der Arbeitsgruppe Theoretische Informatik am Fachbereich Mathematik und Informatik an der Uni Bremen.
Quellen
[1] Kaveh, A. (2022). Introduction to Graph Theory and Algebraic Graph Theory. In: Topological Transformations for Efficient Structural Analysis. Springer, Cham
[2] Flum, J. and Grohe, M. (2006) , Parameterized Complexity Theory. Springer, Berlin









sehr gut erklärt – das hätte ich so nicht rausbekommen