Von Pascal Dinglinger
 Abbildung 1 – Zunge des Thwaites (Doomsday) Gletschers in der Westantarktis. Seine Fläche ist mehr als doppelt so groß wie Österreich und er gilt als wichtiger Indikator für die Auswirkungen des Klimawandels. Aus diesem Grund ist der Gletscher im Fokus einer Vielzahl von Untersuchungen mittels mathematischer Modellierung wie zum Beispiel durch die International Thwaites Glacier Collaboration (ITGC). [1]
Abbildung 1 – Zunge des Thwaites (Doomsday) Gletschers in der Westantarktis. Seine Fläche ist mehr als doppelt so groß wie Österreich und er gilt als wichtiger Indikator für die Auswirkungen des Klimawandels. Aus diesem Grund ist der Gletscher im Fokus einer Vielzahl von Untersuchungen mittels mathematischer Modellierung wie zum Beispiel durch die International Thwaites Glacier Collaboration (ITGC). [1]
Was haben Brücken, Flugzeuge und Klima gemeinsam? Sie alle lassen sich durch verschiedene mathematische Modelle beschreiben. Doch wie genau funktionieren diese Modelle und welche Rolle spielt die Mathematik dabei? Begleite uns auf einer kleinen Reise durch eine Welt voller komplexer Phänomene. Erfahre hier, welche Rolle mathematische Modelle in der Praxis spielen. Wir zeigen euch, wie sie uns helfen können, den Klimawandel besser zu verstehen und Forschern ermöglichen, sogar den Einfluss gigantischer Gletscher wie Thwaites auf den globalen Meeresspiegel zu berechnen.
Der ein oder andere mag sich noch an die mathematischen Werkzeuge der einschlägigen SchülerInnen erinnern: Trigonometrie, binomische Formeln, Kurvendiskussion und vieles mehr. Für die IngenieurInnen und KlimaforscherInnen stellt die mathematische Modellierung eine Kombination aus diesen bekannten und neuen, komplexeren Methoden dar. Die mathematische Modellierung ist dabei wie ein Werkzeugkoffer, welcher das passende Equipment hat, um reale Probleme und Fragen zu behandeln. So werden unter anderem partielle Differentialgleichungen (PDEs) verwendet, um komplexe Systeme mathematisch auszudrücken. Ein Beispiel hierfür ist die Navier-Stokes Gleichung, mit der sich unter anderem Strömungen von Flüssigkeiten und Gasen beschreiben lassen. Mit diesen Werkzeugen lässt sich auch der Klimawandel oder die Schmelze von Gletschern als mathematisches Problem formulieren. [2]
Hierbei gibt es einige spezielle Begriffe, die wir uns genauer ansehen wollen.
Domänen und Systeme – Wo sind wir und was machen wir?
Beim Entwickeln eines mathematischen Modells beginnt man in der Regel mit der Betrachtung der Domäne und des Systems. Doch was bedeuten diese Begriffe eigentlich? Stell dir vor, du bist ein/e ArchitektIn und erhältst den Auftrag, ein Haus zu bauen. Die Domäne ist dabei der Ort, an dem das Haus entstehen soll. Du musst die Bodenbeschaffenheit, die klimatischen Bedingungen und die geltenden Vorschriften verstehen. Erst wenn du die Domäne verstanden hast, kannst du mit dem Entwurf des Hauses beginnen. Das System umfasst dann die konkreten Objekte, wie Steine, Dachziegel und Fenster, aus denen das Haus besteht.
In der mathematischen Modellierung verhält es sich ähnlich. Im Fall des Thwaites Gletschers wird das Gebiet, über das sich der Gletscher erstreckt, als Domäne betrachtet. Bevor die Modellierung beginnen kann, ist ein besseres Verständnis der Domäne erforderlich. WissenschaftlerInnen stützen sich hierbei auf eine Vielzahl von Messungen, etwa von Satellitenbildern oder Exkursionen zum Gletscher. Dabei kommen verschiedene ExpertInnen zusammen, um ihr Domänenwissen zu bündeln.
| Thwaites Gletscher:
Domäne und System des Thwaites Gletschers sind äußerst kompliziert. Der Gletscher umfasst nicht nur ein riesiges Gebiet (192.000 km2) sondern verändert sich auch rasant. Die Oberfläche des Gletschers bewegt sich teils mehr als 2 km pro Jahr und Thwaites trägt allein mit 4 % zum globalen Anstieg des Meeresspiegels bei. Würde er vollständig kollabieren, würden die Ozeane global 65 cm ansteigen. [3] |
Ein mathematisches Modell ist letztlich eine vereinfachte Darstellung eines Systems. Es besteht aus Gleichungen und Variablen, die die Beziehungen zwischen den verschiedenen Elementen des Systems beschreiben. Dabei ist die Domäne nicht nur der Raum, in dem das Modell operiert, sondern sie wird selbst zu einem integralen Bestandteil des Modells. Ziel ist es, das Verhalten des Systems vorherzusagen und zu verstehen, wie es auf verschiedene Änderungen reagieren wird. Eine erfolgreiche Modellierung erfordert daher nicht nur ein tiefes Verständnis der Domäne, sondern auch eine sorgfältige Entwicklung des Modells selbst.
Deterministische Modelle
Zurück zum Klimawandel: Hier gibt es einige Möglichkeiten, was für eine Art Modell wir nutzen. Die bereits erwähnte Navier-Stokes Gleichung wird oft für sogenannte deterministische Modelle eingesetzt. Ein solches Modell beruht auf klar formulierten Beziehungen zwischen Ursache und Wirkung. Zum Beispiel schmilzt ein Eiswürfel wesentlich schneller, je wärmer es in der Umgebung ist. Die Kombination aller möglichen Ursachen und Wirkungen lässt sich ebenfalls mit Gleichungen ausdrücken.
Bei einem deterministischen Modell schaut man sich die Einflüsse an, die den Großteil des Systems ausmachen. WissenschaftlerInnen müssen hierbei die Entscheidung treffen, wie ausführlich das Modell werden soll. Je mehr Einflüsse und Wirkungen im Modell berücksichtigt werden, desto komplexer und schwieriger wird es, das Modell zu berechnen. Hierbei hat jede Komponente einen klar bestimmbaren Einfluss auf das Gesamtsystem. Dieser und ein paar andere Punkte sind für die MathematikerInnen sehr wichtig, um unter anderem zu beweisen, dass ein Modell und die berechnete Lösung eindeutig zueinander passen. Wie solche Vereinfachungen aussehen können, ist zum Beispiel in der folgenden Abbildung zu sehen, wo der Gletscher in kleinere Teile unterteilt wird. Darüber hinaus werden beispielsweise auch unterschiedliche Gleichungen verwendet, um den Einfluss von Reibung zwischen Gletscher und Meeresboden abzuschätzen. Einfachere Gleichungen erleichtern oft die Modellierung erheblich.
| Mathematik in der Anwendung:
Lösungen von PDEs lassen sich mit Methoden wie der Finiten Elemente Methode (FEM) berechnen. Bei dieser wird eine Domäne in viele kleine Teile, die finiten Elemente, unterteilt. MathematikerInnen arbeiten seit einigen Jahrzehnten an der Verfeinerung dieser Methode und dazugehörenden Theorien. Bis heute sind Variationen der FEM und Möglichkeiten zur Abschätzung und Abgrenzung der Fehler Gegenstand der Forschung. Auch in der Uni Bremen gibt es eine Arbeitsgruppe, die in diesem Umfeld forscht (AG Numerik PDE). |
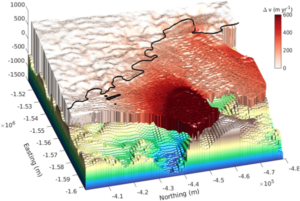
Abbildung 2 – FEM Beispiel der Bewegung des Thwaites Gletschers: Je dunkler ein Bereich, desto schneller bewegt dieser sich. Der Gletscher wird hier in viele kleine Stückchen (Elemente) zerteilt, die zwischen 100 m und 450 m groß sind. Dies vereinfacht die Berechnung des Gesamtmodells. [4]
Stochastische Modelle
Eine gänzlich andere Möglichkeit, mathematische Modelle zu entwickeln, bieten stochastische Modelle. Anders als bei deterministischen Modellen wird hier nicht versucht, eine exakte Lösung mit den getroffenen Annahmen zu berechnen. Stattdessen betrachtet man manche Teile eines Systems als zufällig bzw. variabel. Das kann zum Beispiel genutzt werden, um die Arbeitsleistung einer Gruppe von Menschen zu modellieren. Hierbei könnte eine Person mit einer gewissen Wahrscheinlichkeit krank werden und zeitweise ausfallen. Wenn jemand nun unser Klima modellieren möchte, gibt es viele Faktoren, die wir nicht exakt bestimmen können. Hier ist die Stärke von stochastischen Modellen, dass Unsicherheiten in Messdaten oder Modellparametern in das Modell mit eingebracht werden können. Auf diese Weise kommen häufig unterschiedliche Klimaszenarien zustande, bei denen unbekannte Parameter verändert werden.
Neuronale Netze
Eine besondere Rolle zwischen stochastischen und deterministischen Modellen nehmen künstliche neuronale Netze (KNNs) ein. Diese speziellen Modelle kommen eigentlich aus dem Gebiet des maschinellen Lernens, werden aber auch zu den mathematischen Modellen gezählt. Diese Modelle werden mit bekannten Daten trainiert und “lernen” dadurch Vorhersagen zu machen. Nach diesem Training sind KNNs häufig in der Lage, komplizierte Zusammenhänge nachzubilden und können auch auf neue, unbekannte Daten angewendet werden. Nach dem Training ist ein klassisches KNN deterministisch. Das heißt, dass es bei gleichen Werten das gleiche Ergebnis liefert. Da beim Training jedoch meist zufällige Variationen einfließen, kann ein KNN auch als stochastisches Modell bezeichnet werden.
Das Zentrum für Industriemathematik der Uni Bremen forscht auch an der Nutzung von maschinellem Lernen, um aktuelle Herausforderungen anzugehen. Unter anderem forscht die Arbeitsgruppe Inverse Probleme und Bildverarbeitung an der Verwendung von KNNs, um sogenannte Inverse Probleme zu lösen.
| Zufall im Neuronalen Netz:
Bei neuronalen Netzen werden typischerweise an mehreren Stellen zufällige Variationen eingebracht. Einerseits nimmt man häufig einen zufälligen Anfangszustand, bei dem das Training beginnt. Andererseits werden Trainingsdaten meist zufällig verändert. Dies verbessert oft die Generalisierung und Robustheit eines KNNs. Das bedeutet, es funktioniert nach dem Training oft besser auf neuen, unbekannten Daten, die sich von den Trainingsdaten unterscheiden. |
Mathematische Modellierung an der Uni Bremen
Jetzt haben wir einen kleinen Einblick in eine Auswahl von mathematischen Modellen bekommen. Wer nun denkt “Da habe ich richtig Lust bekommen mehr zu erfahren!” darf sich freuen. Man muss nicht unbedingt Mathe studieren, um diese unterschiedlichen Möglichkeiten zur Beantwortung von Forschungsfragen kennenzulernen. Du kannst zum Beispiel als IngenieurIn die Feinheiten der FEM lernen und damit Strömungen, Energiesysteme oder Gebäude simulieren. [5] Oder siehst du dich eher in den Wirtschaftswissenschaften mit ökonomische Modelle oder versuchst sogar die Rechtssprechung mit Statistik zu verbessern? [6] Oder wer einen Blick in die mathematische Glaskugel werfen will, um die Zukunft unserer Gletscher besser zu verstehen, kann dies im Bereich der Geowissenschaften machen. [7]
Aber das ist noch nicht alles! Diejenigen, die das Thema begeistert, finden in fast allen Disziplinen die Möglichkeit, mathematische Modelle zu nutzen.
Und um die Frage vom Anfang zu beantworten: Flugzeuge, Brücken und auch unser Klima werden alle durch mathematische Modelle beschreibbar. Ob ein neu entworfenes Flugzeug tatsächlich fliegt, eine Brücke auch nach 30 Jahren noch hält oder welcher Hebel heute der effektivste ist, um gegen den Klimawandel vorzugehen – das sind alles komplexe Fragen, bei denen uns die Mathematik das Leben etwas leichter macht und hilft, eine Antwort zu finden.
Quellen & Verweise:
[1]: https://www.jpl.nasa.gov/news/west-antarctic-glacier-loss-appears-unstoppable, zuletzt aktualisiert am 08.04.2023, zuletzt geprüft am 08.04.2023.
[2]: Lorenz, E.N., 1970. Climatic change as a mathematical problem. Journal of Applied Meteorology and Climatology, 9(3), pp.325-329.
[3]: Thwaites Glacier Facts, Online verfügbar unter https://thwaitesglacier.org/about/facts, zuletzt aktualisiert am 01.04.2024, zuletzt geprüft am 01.04.2024
[4]: Weakening of the pinning point buttressing Thwaites Glacier, West Antarctica (2023). Online verfügbar unter https://doi.org/10.5194/tc-16-397-2022, zuletzt aktualisiert am 09.04.2023, zuletzt geprüft am 09.04.2023.
[5]: Strömungsmechanik am ZARM in Bremen: https://www.zarm.uni-bremen.de/de/forschung/stroemungsmechanik.html, zuletzt geprüft am 20.05.2024.
[6]: Empirische Wirtschaftsforschung und angewandte Statistik an der Uni Bremen: https://www.uni-bremen.de/empwifo/forschung, zuletzt geprüft am 20.05.2024.
[7]: Internationale Studie: Wie lässt sich Gletscherschmelze genauer vorhersagen? (2020). Online verfügbar unter https://www.marum.de/Entdecken/Internationale-Studie-Wie-laesst-sich-Gletscherschmelze-genauer-vorhersagen.html, zuletzt aktualisiert am 16.07.2020, zuletzt geprüft am 09.04.2023.








Schreibe einen Kommentar