By Pascal Dinglinger

Figure 1 – The Thwaites (Doomsday) Glacier Tongue in West Antarctica. The extent of its area is more than twice the size of Austria, and it is considered an important indicator of the impacts of climate change. For this reason, The Glacier is the focus of numerous studies using mathematical modeling, such as those conducted by the International Thwaites Glacier Collaboration (ITGC).
What do bridges, airplanes, and climate have in common? They can all be described using various mathematical models. But how exactly do these models work, and what role does mathematics play in them? Join us on a short journey through a world full of complex phenomena. Find out here about the role mathematical models play in practice. We’ll show you how they can help us better understand climate change and enable researchers to calculate the impact of gigantic glaciers like Thwaites on global sea levels.
Some may still remember the mathematical tools from their school days: trigonometry, binomial formulas, curve sketching, and much more. For engineers and climate researchers, mathematical modeling represents a combination of these familiar tools and newer, more complex methods. Mathematical modeling is like a toolbox equipped with the right tools to address real problems and questions. Partial differential equations (PDEs), among other methods, are used to mathematically express complex systems. An example of this is the Navier-Stokes equation, which is used to describe, among other things, the flow of liquids and gases. With these tools, climate change and the melting of glaciers can also be formulated as mathematical problems. [2]
There are some specific terms that we want to take a closer look at.
Domains and systems – Where are we and what are we doing?
When developing a mathematical model, you usually start by looking at the domain and the system. But what do these terms actually mean? Imagine you are an architect and you receive the task of building a house. The domain is the location where the house is to be built. You need to understand the soil composition, the climatic conditions, and the applicable regulations. Only once you have understood the domain can you begin designing the house. The system then includes the concrete objects, such as bricks, roof tiles and windows, that make up the house.
The situation is similar in mathematical modeling. In the case of the Thwaites Glacier, the area over which the glacier extends is considered the domain. Before the modeling can begin, a better understanding of the domain is required. Scientists rely on a variety of measurements for this, such as satellite images or expeditions to the glacier. Various experts come together to combine their domain knowledge.
|
Thwaites Glacier: The domain and system of the Thwaites Glacier are extremely complex. The glacier covers not only a huge area (192,000 km2) but is also changing rapidly. The surface of the glacier moves at a rate of more than 2 kilometers per year in some areas, and Thwaites alone contributes 4% to the global rise in sea levels. If it were to completely collapse, the oceans would rise globally by 65 centimeters. [3] |
A mathematical model is ultimately a simplified representation of a system. It consists of equations and variables that describe the relationships between the various elements of the system. The domain is not only the space in which the model operates, but it becomes an integral part of the model itself. The goal is to predict the behavior of the system and understand how it will respond to various changes. Successful modeling therefore requires not only a deep understanding of the domain but also careful development of the model itself.
Deterministic Models
Back to climate change: There are several options for the type of model we can use. The previously mentioned Navier-Stokes equation is often used for so-called deterministic models. Such a model is based on clearly defined relationships between cause and effect. For example, an ice cube melts much faster the warmer the surrounding environment is. The combination of all possible causes and effects can also be expressed with equations.
In a deterministic model, one looks at the influences that make up the majority of the system. Scientists must make the decision on how detailed the model should be. The more influences and effects are taken into account in the model, the more complex and difficult it becomes to calculate the model. Each component has a clearly measurable influence on the overall system. This and a few other points are very important for mathematicians, in order to prove that a model and the calculated solution match uniquely with each other. An example of such simplifications can be seen in the following illustration, where the glacier is divided into smaller sections. In addition, different equations are also used, for example, to estimate the impact of friction between the glacier and the seabed. Simpler equations often make modeling considerably easier.
|
Mathematics in application: Solutions to partial differential equations (PDEs) can be computed using methods such as the Finite Element Method (FEM). In this method, a domain is divided into many small parts, called finite elements. Mathematicians have been working for several decades on refining this method and the associated theories. To this day, variations of the FEM and methods for estimating and bounding errors remain a focus of research. There is also a working group at the University of Bremen that works in this field (WG Numerics of PDEs). |
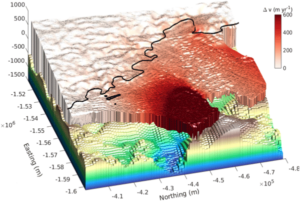
Figure 2 – FEM example of the movement of the Thwaites Glacier: The darker an area, the faster it moves. The glacier is divided into many small pieces (elements), each ranging in size from 100 m to 450 m. This simplifies the calculation of the overall model.[4]
Stochastic Models
Stochastic models offer a completely different way of developing mathematical models. Unlike deterministic models, the goal here is not to calculate an exact solution based on the assumptions made. Instead, some parts of a system are considered random or variable. This can be used, for example, to model the work performance of a group of people. In this case, a person might become sick with a certain probability and temporarily be absent. If someone wants to model our climate, there are many factors that we cannot determine exactly. This is where the strength of stochastic models lies: uncertainties in measurement data or model parameters can be incorporated into the model. In this way, different climate scenarios often arise, where unknown parameters are varied.
Neural Networks
Artificial neural network (ANNs) play a special role between stochastic and deterministic models. These special models actually come from the field of machine learning, but they are also classified as mathematical models. These models are trained with known data and “learn” to make predictions. After this training, ANNs are often capable of replicating complex relationships and can also be applied to new, unknown data. After training, a classic ANN is deterministic. This means that it provides the same result for the same input values. However, since random variations are often introduced during training, an ANN can also be considered a stochastic model.
The Center for Industrial Mathematics at the University of Bremen also conducts research on the use of machine learning to address current challenges. Among other things, the Inverse Problems and Imaging Working Group is researching the use of ANNs to solve so-called inverse problems.
|
Randomness in the Neural Network: In neural networks, random variations are typically introduced at several points. On one hand, a random initial state is often used to start the training process. On the other hand, training data is often randomly modified. This often improves the generalization and robustness of a ANNs. This means that after training, it often performs better on new, unseen data that differs from the training data. |
Mathematical Modeling at the University of Bremen
Now we have had a brief glimpse into a selection of mathematical models. Anyone who thinks, “I’m really excited to learn more!” will be pleased. One doesn’t necessarily have to study math to explore these different methods of answering research questions. For example, as an engineer, you can learn the intricacies of FEM and use it to simulate fluid dynamics, energy systems, or buildings.[5] Or do you see yourself more in the field of economics with economic models, or even trying to improve jurisprudence statistics? [6] Or if you want to take a look into the mathematical crystal ball to better understand the future of our glaciers, you can do so in the field of geosciences. [7]
But that’s not all! Those who are excited about the topic can find opportunities to use mathematical models in nearly every discipline.
And to answer the question from the beginning: Airplanes, bridges, and even our climate can all be described by mathematical models. Whether a newly designed airplane will actually fly, whether a bridge will still hold up after 30 years, or which lever is the most effective today to combat climate change – these are all complex questions where mathematics makes life a little easier and helps us find an answer.
Sources
[1]: https://www.jpl.nasa.gov/news/west-antarctic-glacier-loss-appears-unstoppable, zuletzt aktualisiert am 08.04.2023, zuletzt geprüft am 08.04.2023.
[2]: Lorenz, E.N., 1970. Climatic change as a mathematical problem. Journal of Applied Meteorology and Climatology, 9(3), pp.325-329.
[3]: Thwaites Glacier Facts, Online verfügbar unter https://thwaitesglacier.org/about/facts, zuletzt aktualisiert am 01.04.2024, zuletzt geprüft am 01.04.2024
[4]: Weakening of the pinning point buttressing Thwaites Glacier, West Antarctica (2023). Online verfügbar unter https://doi.org/10.5194/tc-16-397-2022, zuletzt aktualisiert am 09.04.2023, zuletzt geprüft am 09.04.2023.
[5]: Strömungsmechanik am ZARM in Bremen: https://www.zarm.uni-bremen.de/de/forschung/stroemungsmechanik.html, zuletzt geprüft am 20.05.2024.
[6]: Empirische Wirtschaftsforschung und angewandte Statistik an der Uni Bremen: https://www.uni-bremen.de/empwifo/forschung, zuletzt geprüft am 20.05.2024.
[7]: Internationale Studie: Wie lässt sich Gletscherschmelze genauer vorhersagen? (2020). Online verfügbar unter https://www.marum.de/Entdecken/Internationale-Studie-Wie-laesst-sich-Gletscherschmelze-genauer-vorhersagen.html, zuletzt aktualisiert am 16.07.2020, zuletzt geprüft am 09.04.2023.








Leave a Reply