In diesen Spielversionen geht es darum, die Auswirkungen von Konkurrenz zwischen zwei Arten zu betrachten. Dies geschieht zum einen durch direkte Betrachtung der erspielten Ergebnisse. Zum anderen werden aus den Ergebnissen Parameter ermittelt, die dann in das Konkurrenzmodell von Lotka-Volterra eingesetzt werden können. Dies ermöglicht grundsätzliche Aussagen zur Konkurrenzbeziehung der betrachteten Arten.
Grundlage für die Analysen sind Daten aller Konkurrenz-Spielversionen.
Aufgabe 3.1)
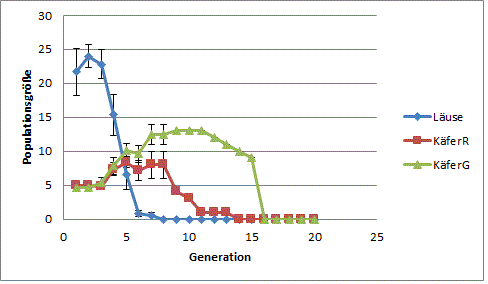
Stellen Sie in Abb. 3.1 (Siebenpunkt-Marienkäfer vs. Asiatische Marienkäfer) und Abb. 3.2 (Marienkäfer vs. Schlupfwespen) den Zusammenhang zwischen Zeit t (=Anzahl Spielrunden bzw. Generationen) und Populationsgrößen N grafisch dar. Verwenden Sie dazu die in jeder Generation vorhandenen Blattläuse, sowie die Anzahlen der jeweils adult vorhandenen Gegenspieler. Nutzen Sie die Mittelwerte (MW) aller Ihnen zur Verfügung stehenden Daten (MW Generation1, MW G2 usw. und fügen die zugehörigen Standardfehler mit ein.
Aufgabe 3.2)
Ein gutes Modell, mit dem zwischenartliche Konkurrenz beschrieben werden kann, basiert auf der bereits bekannten Gleichung für logistisches Wachtum: dN/dt = r* N*((K-N)/K). Um diese Gleichung nun für die Beschreibung von Konkurrenzeffekten nutzen zu können, muss man die Konkurrenzstärke der einen Art in „Konkurrenzeinheiten“ der anderen Art umrechen. Ein Individuum von Art 1 hat auf ein anderes der Art 1 den gleichen Effekt, wie ihn zum Beispiel 3 Individuen der Art 2 hätten (N1 = N2/3). Fügen wir den Konkurrenzkoeffizienten a12 in die logistische Gleichung ein, ergibt sich folgendes für Art 1:
dN1/dt = r1* N1*((K1-N1-a12*N2)/K1)
Und analog für Art 2:
dN2/dt = r2* N2*((K2-N2-a21 N1)/K2)
Bestimmen Sie nun die zugehörigen Parameter:
a) N1 und N2 sind die Populationsgrößen von Art 1 bzw. Art 2. Lesen Sie diese aus den Abbildungen 1 bzw. 2 ab. Nehmen Sie hierzu den maximalen Wert der ersten Populationsspitze.
b) r1 und r2 sind die intrinsischen Wachstumsraten. Sie können Sie analog zu Aufgabe 1.2, intraspezifische Konkurrenz, bestimmen. Vergleichen Sie die unter Konkurrenz ermittelten Wachstumsraten des Siebenpunkt-Marienkäfers mit der Wachstumsrate, die Sie im Räuber Beute Experiment ermittelt haben, in dem der Marienkäfer allein vorkam.
c) K1 und K2 entsprechen wiederum der Habitatkapazität. Diesen Wert können Sie nicht unter Konkurrenzbedingungen bestimmen. Schauen Sie daher in die Experimente zur Räuber-Beute-Beziehung und lesen Sie KSchlupfwespe und KMarienkäfer dort ab. K ist für beide Marienkäferarten gleich.
Aufgabe 3.3)
a12 und a21 sind die sogenannten Konkurrenzeffizienten. Damit wird die Stärke von Art 1 in Konkurrenzeinheiten zu Art 2 ausgedrückt und umgekehrt. Sie zu berechnen ist etwas komplexer: Wenn Population 1 K1 erreicht hat, kann sie nicht weiter wachsen, daher ist dN1/dt = 0.
Unter diesen Umständen gilt auch: K1-N1-a12*N2 = 0.
Unter Anwendung von ein wenig Algebra ergibt sich:
a12 = (K1 – N1)/ N2.
Nun muss man nur noch entsprechend die in Aufgabe 3.2) bestimmten Werte für K1 , N1, und N2 einsetzen und erhält so a12. Die Berechnung für a21 ergibt sich analog.
Aufgabe 3.4)
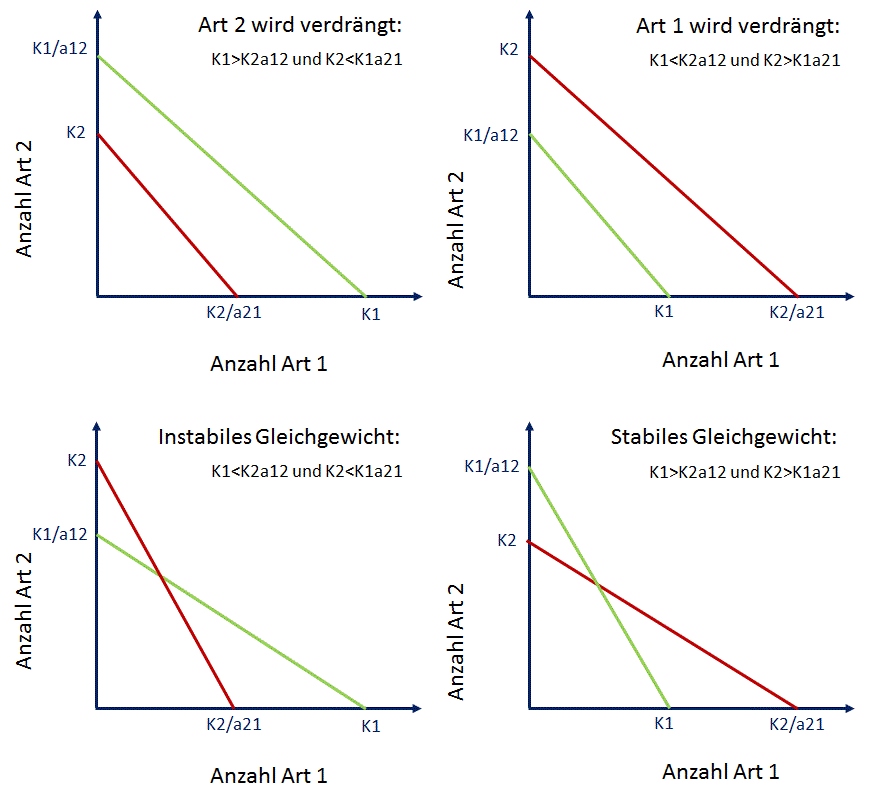
Tragen Sie, einmal für die beiden Marienkäferarten und einmal für die Marienkäfer-Schlupfwespen Interaktion, die unter Aufgabe 2 berechneten Werte so in ein Diagramm ein, dass Sie eines der hier stehenden Beispieldiagramme erhalten. Beachten Sie dabei den Aufbau der Wertetabelle, damit die Darstellung der Isoklinen funktioniert.
| Art1 x | Art1 y | Art2 x | Art2 y | |
| 0 | K1/a12 | K2/a21 | 0 | |
| K1 | 0 | 0 | K2 |
Aufgabe 3.5)
Lesen Sie aus den erhaltenen Grafiken ab, welche Vorhersagen für die jeweilige Konkurrenzsituation gemacht wird. Wird Art 1 Art 2 immer ausrotten? Gibt es stabile Koexistenz oder ein instabiles Gleichgewicht? Oder wird Art 2 stets Art 1 auslöschen? Argumentieren Sie anhand der Größenverhältnisse von K1 zu K2* a12 bzw. K2 zu K1*a21. Nutzen Sie hierzu ein Lehrbuch der Ökologie oder Populationsökologie und geben Sie diese Quelle korrekt an.
Aufgabe 3.6)
Betrachten Sie nun die Konkurrenzsituation zwischen den beiden Marienkäferarten bzw. zwischen Marienkäfer und Schlupfwespe wenn es zu Störungen durch das Auftreten der Florfliegenlarve kommt.
a) Haben Störungen einen stabilisierenden oder destabilisierenden Effekt? Dokumentieren Sie je ein Beispiel für die beiden Käferarten bzw. Käfer und Schlupfwespe mit Hilfe einer aussagekräftigen Abbildung.
b) Was sagt ihr Lehrbuch bezüglich des Effekts von Störungen?
Aufgabe 3. 7)
Würden Sie nun, wenn Sie Blattläuse effizient bekämpfen müssten, einen Nüzling einsetzen oder zwei gleichzeitig? Welche Art(en) würden Sie wählen? Argumentieren Sie basierend auf den berechneten Werten bzw. verweisen Sie entsprechend auf ihre erstellten Abbildungen.