In diesen Aufgaben geht es vor allem darum, wichtige Parameter der interspezifischen Konkurrenz innerhalb von Populationen zu verstehen. Als Grundlage dienen die Daten des Spiels „Kapazitätsgrenze“.
Aufgabe 1.1)
Notieren Sie, welche Bedeutung dem Standardfehler zukommt, wenn man Datenpunkte miteinander vergleichen möchte. Wieso wird der Standardfehler normalerweise mit der zunehmenden Anzahl von Versuchswiederholungen kleiner?
Aufgabe 1.2)
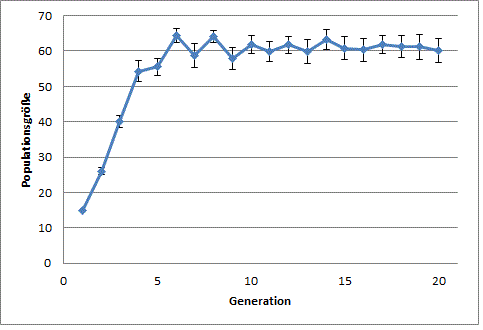
Stellen Sie in Abb. 1.1 den Zusammenhang zwischen Zeit t (=Anzahl Spielrunden bzw. Generationen) und Populationsgröße N (Summe aller vorhandenen Blattlausstadien) grafisch dar. Verwenden Sie dazu die Mittelwerte (MW) aller Ihnen zur Verfügung stehenden Daten (MW Generation1, MW G2 usw. und fügen die zugehörigen Standardfehler mit ein.
Aufgabe 1.3)
Der Beitrag eines Individuums zum Populationswachstum wird durch die durchschnittliche Wachstumsrate per capita mit dN/dt * 1/N beschrieben. Ohne begrenzende Ressourcen ist diese Rate eine Konstante, was dem Maximum an Zuwachs entspricht. Sie wird auch als spezifische natürliche Wachstumsrate r bezeichnet:
r = dN/dt * (1/N) (A)
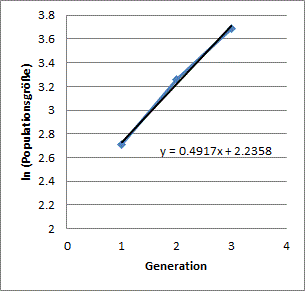
Zur Bestimmung von r wird analog zu 1) eine grafische Auftragung angefertigt (Abb. 1.2), aber mit dem natürlichen Logarithmus der Populationsgröße (lnN) und nur für die Generationen 1-3. Man sollte eine Gerade erhalten, deren Steigung r entspricht.
Tipp: Regressionsgerade samt Formel anzeigen lassen, so dass sich die Steigung einfach ablesen lässt.
Aufgabe 1.4)
Ergänzen Sie Abbildung 1) um ein Populationsökologisches Modell, welches auf der Annahme exponentiellen Wachtums beruht (dN/dt = r* N). Während r eine Konstante ist, verändert sich die Populationsgröße N mit jedem Generationsschritt, dN/dt gibt die Veränderung pro Schritt an. Die Populationsgröße im zweiten Schritt (t2) berechnet sich also folgendermaßen:
N2 = r*N1 + N1 (B)
Die Populationsgröße im dritten Schritt (t3) entsprechend:
N3 = r*N2 + N2 (C)
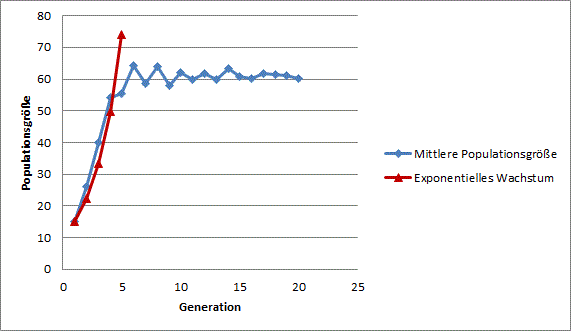
Führen Sie diese Berechnungen für die ersten fünf Generationsschritte durch und tragen sie die so berechneten Populationsgrößen gegen die Zeit auf (zu Abb. 1.1 hinzufügen).
Aufgabe 1.5)
a) Bei begrenzten Resourcen kommt intraspezifische Konkurrenz zum Tragen. Das Populationswachstum wird limitiert und die Populationsgröße schwankt um die Kapazitätsgrenze K.Lesen Sie K bestmöglich aus Abbildung 1.1 ab.
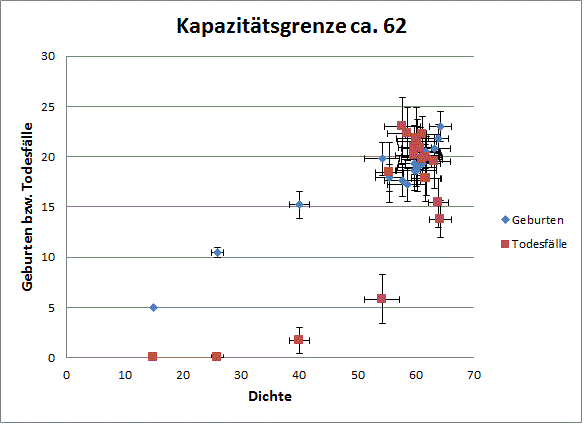
b) Tragen Sie außerdem für die ersten 10 Generationen sowohl die Geburten als auch die Todesfälle (Verluste) gegen die Gesamtzahl vorhandener Blattläuse (N) auf (Abb. 1.3). Tragen Sie dabei sowohl die Standardfehler der Geburten bzw. Todesfälle auf (senkrechte y-Fehlerbalken), als auch die der zugehörigen Populationsgrößen (waagerechte x-Fehlerbalken). An der Kapazitätsgrenze sind Geburten- und Sterberate gleich; lesen Sie den Wert ab.
c) Berechnen Sie nun K, indem Sie die Populationsgrößen N der Generationsschritte 6-20 mitteln. Liegen die a) und b) grafisch ermittelten Werte im Bereich des Standardfehlers des berechneten Wertes? Interpretieren Sie den Befund.
Aufgabe 1.6)
Ergänzen Sie Abbildung 1) um ein Populationsökologisches Modell, welches auf der Annahme logistischen Wachtums beruht (dN/dt = r* N*((K-N)/K). Wiederum ändert sich N mit der Generation, während r und K Konstanten sind. Die Populationsgröße im zweiten Schritt (t2) berechnet sich also folgendermaßen:
N2 = r*N1 *((K- N1)/K) + N1 (D)
Die Populationsgröße im dritten Schritt (t3) entsprechend:
N3 = r*N2 *((K- N2)/K) + N2 (E)
Führen Sie diese Berechnungen für alle 20 Generationsschritte durch und tragen sie die berechnete Populationsgröße gegen die Zeit auf (zu Abb. 1.1 dazu).
Was passiert, wenn Ihre Ausgangs-Populationsgröße N1 größer ist als K und z.B. 250 Individuen beträgt? Erstellen Sie eine illustrierende Abbildung.
Aufgabe 1.7)
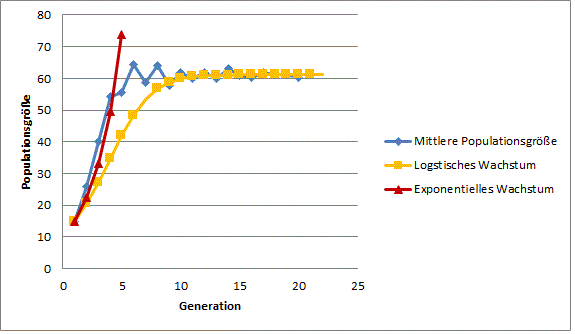
Vergleichen Sie die drei Wachstumskurven in Abbildung 1.1 und interpretieren Sie Ähnlichkeiten und Unterschiede.
Aufgabe 1.8)
Störungen können, wie der Name schon sagt, ein ökologisches System ganz schön aus dem Gleichgewicht bringen.
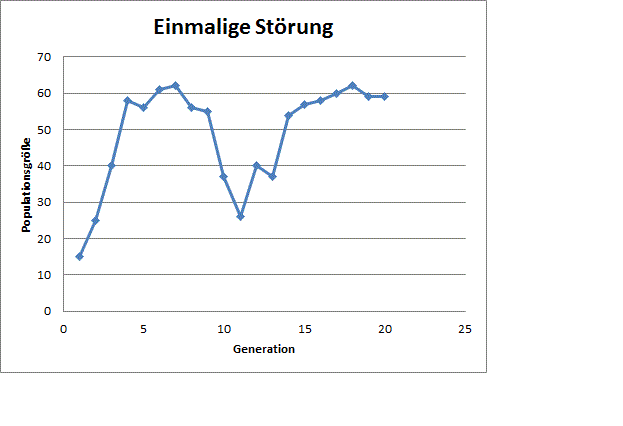
Wie wirkt sich das Vorkommen von Störungen (Larve der Florfliege) auf das Erreichen der Kapazitätsgrenze aus? Stellen Sie aussagekräftige Einzelfall-Abbildungen (keine Mittelwerte) für das einmalige, zweifache und, wenn vorhanden, dreifache Auftreten der Larve während des Spielverlaufs dar.
Aufgabe 1.9)
In einer reinen Blattlauspopulation, wie schnell ist das Gleichgewicht nach einer Störung wieder hergestellt? Und bei welcher Störungsfrequenz ergeben sich wohl chaotische Populationsschwankungen?

Die Spielidee ist super, doch warum enthält diese Seite und die Anleitung und manchen Stellen Rechtschreibfehler? Zudem wundert es mich, warum die Abbildungen stellenweise sehr verpixelt dargestellt sind. Von einer Uni könnte man erwarten, dass solch schönen Ideen mehr „wie aus einem Guss“ umgesetzt werden. Ich habe die Abbildungen neugezeichnet und die Anleitungen neu geschrieben. So ist es für Schüler auch motivierender damit umzugehen, wenn gesehen wird, dass das Material – dem Anschein nach – nicht amateurhaft zusammengeklöppelt ist.
Lieber Herr Weninger,
ja, niemand ist perfekt… Und auch wir sind nur Menschen mit vielen weiteren Verpflichtungen, die, neben der regulären Arbeit, dieses Spiel auch noch öffentlich im Netz verfügbar gemacht haben. Fein, wenn Sie es perfektioniert haben. Dazu ist es da, damit jeder es so weiter entwikeln kann, wie es passt. Ist Ihre verbesserte Version auch öffentlich verfügbar? Das wäre doch schön.
Beste Grüße
A. Thiel